数学中的概率论是研究随机现象数量规律的数学分支。在概率论的系统中，根据事件发生的可能性，将事件分成必然事件，不可能事件和随机事件。例如在正常状态下，抛掷一枚硬币，可能出现正面或者反面，这是一个不确定的事件，属于随机事件，而硬币会落下，就是肯定会发生的事件，属于必然事件。

我们结合数字型彩票的开奖：以福彩3d为例，开奖号的号码一共有0到9十个号码，那么随便开出一个号码，开出0到9之中的数字就是必然事件，开出10这个号码就是不可能事件，开出7这个号码就是随机事件了。

在彩票预测中，必然事件和不可能事件没有研究的价值，彩票们关注也就是对于随机事件的研究了。

数字型彩票中的概率其实就是传统概率，也被叫作拉普拉斯概率。在拉普拉斯试验中，所包含的单位事件是有限的，且每个单位事件发生的可能性均相等。在数字型彩票中，开出的号码的总数是一样的，每个号码被开出的可能性也是一样的。

在彩票预测中，必然事件和不可能事件没有研究的价值，彩票们关注也就是对于随机事件的研究了。

数字型彩票中的概率其实就是传统概率，也被叫作拉普拉斯概率。在拉普拉斯试验中，所包含的单位事件是有限的，且每个单位事件发生的可能性均相等。在数字型彩票中，开出的号码的总数是一样的，每个号码被开出的可能性也是一样的。

但这并不是意味着，概率学理论在彩票的具体运用中没有任何作用。数字型彩票的开奖虽然从长远来看，每个号码摇出的次数是基本相等的，看起来是一个完全随机的过程，没有分析号码的必要，但是我们经常可以发现在某一特定时期内，开奖号码的开奖规律却是有迹可循的。这是为什么呢？

因为在现实生活中，绝对随机数是不存在，我们说的各种随机数其实都是相对随机数，也就是伪随机数，因为在现实中，随机数的产生不是凭空的，它需要依靠各种载体，比如电脑之类。彩票的摇奖也是一样，受到摇奖机的设置、彩球的制作、彩球的大小、重点、表面光滑程度、摇奖室内各项指标的差异等等人为因素影响，因此彩票的开奖其实是一个伪随机数，伪随机数在有些时候是有规律可循的，可以把握和预测。

那么对于广大的彩民来说，寻找出开奖号码一段时期内的规律和走势才是最重要的。这里我们又要提到一个新的名词——偏态。

偏态，指的是非对称分布的偏斜状态。换句话说，就是统计数据的峰值与平均数不相等的频率分布。而与偏态相对的则是正态分布，也可以叫做常态分布。                正态分布有两个参数，即期望（均数）μ和标准差σ，它的分布曲线表现为中间高，两侧逐渐均匀下降，左右对称，呈钟形。               当样本数量增大时，偏态分布的均数会慢慢趋向于正态分布。               在基于偏态理论的基础上，我们可以通过多种分类方法，对已经摇出的彩票中奖号码进行统计，然后再根据每种分类方法中彩票号码显现出来的走势，对后面几期的开奖结果进行预测了。              当然在彩票领域，偏态理论最直接的运用，就是偏态指数了。偏态指数=遗漏期数÷理论周期x100%，通过历史的数据来看，每次当偏态指数达到500%的时候，就可以对该号码进行追捧了。

比如在福彩3d的2016194期的时候，4号球的遗漏期数为11期，而在近100期内4号球的平均遗漏期数只有2期，偏态指数=遗漏期数÷理论周期x100% = 550%，已经超过了500%，所以在后面的几期开奖中，我们可以追捧4号球了，而在第2016194期的时候3d开奖开出了407，成功开出了4号球。

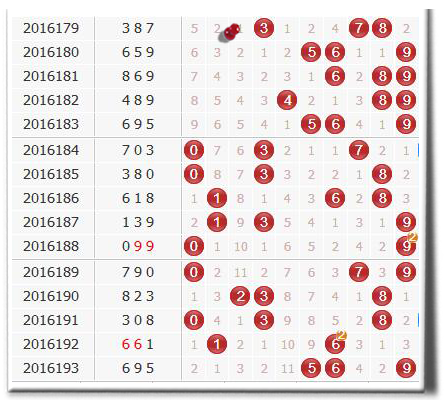
同样的，在大盘玩法双色球中，偏态公式同样适用，比如第2016076期的双色球开奖，红球中，30号球遗漏了30期，而在近50期内30号球的平均遗漏周期是5期，偏态指数已经达到了600%，最后很快30号球在第2016076期的时候开了出来。

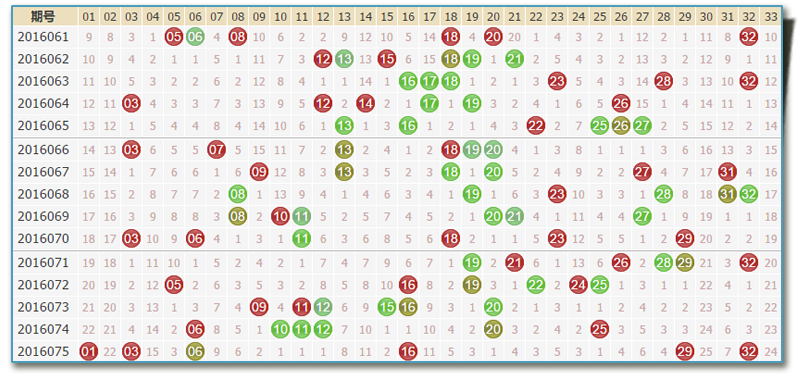
当然并不是每期都会有偏态指数超过500%的号码存在，但也因为这样，缩减了我们的资本投入，而当符合条件的号码出现后，我们要抓住机会，把资本用到刀刃上。如果能通过偏态理论来分析短期内的彩票走势，把握住伪随机数中稍纵即逝的规律，那离中奖就不远了。